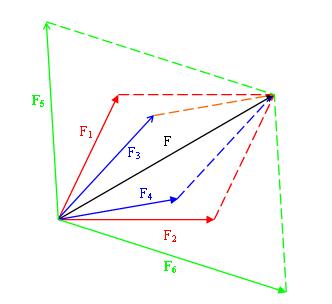
本套课程为8年级物理专题-力的合成与分解教学视频，这个章节是学习物理力学基础核心课程，能否学好这个章节课程将影响后期力学学习。
.合力和力的合成：一个力产生的效果如果能跟本来几个力共同作用产生的效果相同，这个力就叫那几个力的合力，求几个力的合力叫力的合成． 　2.力的平行四边形定则：求两个互成角度的共点力的合力，可以用表示这两个力的线段为邻边作平行四边形，合力的大小和标的目的就可以用这个平行四边形的对角线表示出来。
共点的两个力F1，F2的合力F的大小，与它们的夹角θ(0≤θ≤π)有关，θ越大，合力越小；θ越小，合力越大，合力可能比分力大，也可能比分力小，F1与F2同向时合力最大，F1与F2反向时合力最小，合力大小的取值范围是|F1－F2|≤F≤（F1+F2）（当θ=120°时，合力=分力）
力的合成和分解  1．原则：等效替代。
用一个力等效代替几个力叫力的合成，用几个力等效代替一个力叫力的分解。   合力和分力是等效替代关系，即合力和分力的作用效果相同。
  在对物体进行受力分析时，考虑了合力就不考虑分力，考虑了分力就不考虑合力，因为它们是等效替代关系。 2．方法：
  平行四边形法则、解三角形(主要是直角三角形)、公式法、正交分解法  3、力的合成
  ⑴．同一直线上两力的合成 先规定正标的目的，转化为代数运算。 同向两力的合成：相加。(合力最大)
  反向两力的合成：大力减小力，合力标的目的与大力标的目的相同。(合力最小)   本色：规定正标的目的后，加上一个“负”的力。(《金版教程》P15)1   ⑵．互相垂直的两力的合成：解直角三角形。
4、力的分解
⑴．斜面上重物的重力的分解：      F1=mgsinθ    F2=mgcosθ 注意：这种分解并不是绝对的。如图。
 
分解力时，要按照力的实际作用效果来分。 ⑵．斜向上方（或斜向下方）的力的分解：      F1=Fcosθ    F2=Fsinθ
⑶．正交分解：正交分解法求合力，在解决多个力的合成时，有明显的优点。在运用牛顿第二定律解题时常常用到。
建立直角坐标系，将力向两个坐标轴分解，转化为同一直线上的力的合成。 5．合力和分力的关系
  ①．合力与分力是从力对同一物体产生的作用效果相同来定义的，因此，作用在不同物体上的力，不能合成，因为它们的作用效果不会相同。
②．一个力被合力(或分力)替代后，本身不再参与计算，以免重复。 ③． 合力不必然大于分力。合力既可能大于分力，也可能等于或小于分力。
三．用平行四边形法则解题
正交分解法是解决力学问题的基本方法，这种方法往往较繁琐，要求有较好的数学功底，容易因粗心而出错。
平行四边形法则是一种较简洁的解题方法。在解决三力作用下物体的平衡问题时，灵活运用此法可以使解题过程大大简化。
平行四边形法常常转化为三角形法。
［例1］两个共点力的合力与分力的关系是 ［ ］ A．合力大小必然等于两个分力大小之和 B．合力大小必然大于两个分力大小之和 C．合力大小必然小于两个分力大小之和
D．合力大小必然大于一个分力的大小，小于另一个分力的大小
E．合力大小可能比两个分力的大小都大，可能都小，也可能比一个分力大，比另一个分力小 ［分析］因为两个共点力合力的大小范围是
 
所以情况B不成能，情况A、C、D不必然． ［答］E．  
［例2］大小为4N、7N和9N的三个共点力，它们的最大合力是多大？最小合力是多大？ ［误解］当三个力同标的目的时，合力最大，此时，F合=20N。当4N、7N的两个力同向且与9N的力标的目的相反时，合力最小，此时F合=2N。
［正确解答］当三个力同标的目的时，合力最大，合力最大值为F=F1+F2+F3=20N。
由于这三个力中任意两个力的合力的最小值都小于第三个力，所以这三个力的合力的最小值为零。
［错因分析与解题指导］［误解］在求三个共点力最小合力时，由于思维定势的负作用，仍和求最大合力一样，把三个力限定在一直线上考虑，从而导致错误。
共点的两个力（F1，F2）的合力的取值范围是｜F1-F2｜≤F合≤F1+F2。若第三个共点力的大小在这一范围内，那么这三个力的合力可以为零。必需指出，矢量的正负号是用来表示矢量的标的目的的，比力两个矢量的大小应比力这两个矢量的绝对值，而不该比力这两个力的代数值。  
［例3］在同一平面上的三个共点力，它们之间的夹角都是120°，大小别离为20N、30N、40N，求这三个力的合力．
［分析］求两个以上共点力的合力，可依次应用平行四边形法则．为此可先求出F1、F2的合力F′，再求F′与F3的合力（图1）．由于需计算F′与F2的夹角θ，显得较繁琐．
比力便利的方法可以先分解、后合成——把F2分成20N+10N两个力，F3分成20N+20N两个力．因为同一平面内互成120°角的等大小的三个共点力的合力等于零，于是原题就简化为沿F2标的目的一个10N的力（F′2）、沿F3标的目的一个20N的力（F′3）的合